等比数列解题的基本思路是什么
哇塞,等比数列题目看起来复杂,但其实掌握几个关键公式就能轻松搞定!首先得记住通项公式an=a1*q^(n-1)和求和公式Sn=a1(1-q^n)/(1-q)。遇到题目时先别慌,把已知条件列出来,看看能推出什么关系。比如说已知a3和a5,就可以用a5/a3=q²来求公比。有时候方程会出现高次项,像六次方程这种,高中阶段一般不会要求解全,很可能有特殊解比如q=1。
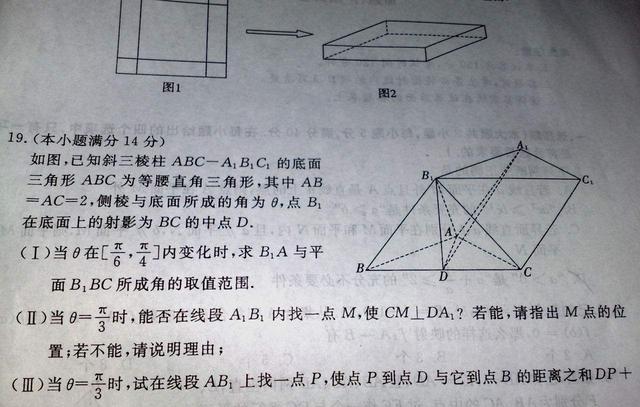
具体解题步骤和方法详解
-
知三求二法:等比数列中只要知道任意三个量,就能求出另外两个。比如知道a1、an、Sn,就能求q和n。举个栗子,a1=1/2,an=243/2,Sn=182,通过an/a1=q^(n-1)=243,发现243是3的5次方,所以n-1=5,n=6,再代入求和公式就能求q。
-
整体代换技巧:有些题目需要巧妙变形。比如a3a5+a2a10+2a4a6=100,利用性质a3a5=a4²,a2a10=a6²,就能化成(a4+a6)²=100,再结合an>0的条件,得到a4+a6=10。是不是很巧妙?
-
方程组求解:当给出两个条件时,往往要联立方程。比如a2+a5=18和a3+a6=9,可以提取公因式得到a1q(1+q³)=18和a1q²(1+q³)=9,两式相除就能求出q=1/2,再代回求a1=32。最后解an=1,即32*(1/2)^(n-1)=1,得到n=6。
-
递推关系应用:已知a5=4,a7=9,求a9。不需要求a1,直接用a7/a5=q²=9/4,那么a9=a7q²=9(9/4)=81/4。看,跳着求更快捷!

相关问题解答
-
等比数列最常见的解题误区有哪些?
哎呀,同学们最容易栽跟头的地方就是公式记混啦!经常有人把等比数列和等差数列的公式搞混,还有就是在使用求和公式时忘记讨论q=1的情况。另外看到高次方程就发怵,其实很多时候都有特殊解。最重要的是,没注意题目隐含条件,比如各项均为正数,这些细节决定成败啊! -
如何快速判断等比数列的题目类型?
嘿嘿,这个有窍门!如果题目给出连续两项的关系,很可能要用通项公式;如果涉及求和,自然要用Sn的公式;如果给出不相邻的项,比如a3和a5,就要用比值关系;如果给出两个条件,大概率要解方程组。多练几道题,你就能一眼看出套路啦! -
遇到复杂的等比数列题应该怎么办?
别怕别怕!先深呼吸,把已知条件一个个写出来。然后想想能用哪个公式,有时候需要把条件变形一下。如果出现高次方程,先试试有没有明显解,比如q=1或q=-1。实在不行就把方程两边同时除以某个因式简化。记住,高中数学不会出太变态的题,肯定有解法的! -
怎样验证等比数列的答案是否正确?
好问题!最简单的方法就是代回原题验证。比如求出q和a1后,可以算算其他项是否符合条件。也可以检查求和是否正确。有时候用不同方法计算同一个量,看结果是否一致。对了,还要注意题目有没有特殊限制,比如"各项为正"或"q≠1"等,确保答案符合所有条件哦!






新增评论