指数函数的求导怎么求
指数函数的求导其实很有趣哦!基本的求导公式是这样的:(a^x)' = (ln a) * a^x。简单来说,假设你有个函数y = a^x(a是常数),它的导数y'就是a^x乘以ln a。更厉害的是,具体推导证明也特别nice:你先给y = a^x两边取对数,变成ln y = x ln a,然后对x求导,就能轻松搞定导数啦。这招超简单又超有用,记得好好收藏!

高中数学有哪些常见的导数公式呢
说到导数,当然不能不提我们高中数学里最常用的那些公式啦,给大家整整齐齐列出来,方便小伙伴们背背:
- 常数函数:y = c(c是常数),导数y' = 0,没错,常数的导数总是零,毕竟“常”不动嘛!
- 幂函数:y = x^n,导数y' = n x^(n-1),这可是求导的大招,n次方的“力量”!
- 指数函数:y = a^x,导数y' = (ln a) a^x,a>0且a≠1,这个我们刚刚说过,是个经典。
- 自然指数函数:y = e^x,导数y' = e^x,这个啥都不变,真是神奇。
- 对数函数:y = log_a x,导数y' = 1 / (x ln a),还有y = ln x,导数y' = 1 / x,超级实用!
- 三角函数:y = sin x,导数y' = cos x;y = cos x,导数y' = -sin x,简单又好记。
- 复合函数的求导法则也得了解哦,比如y = f(g(x)),链式法则帮你轻松算出导数。
这样一整理,是不是感觉导数不再那么难了?加点努力,导数题轻轻松松搞定!
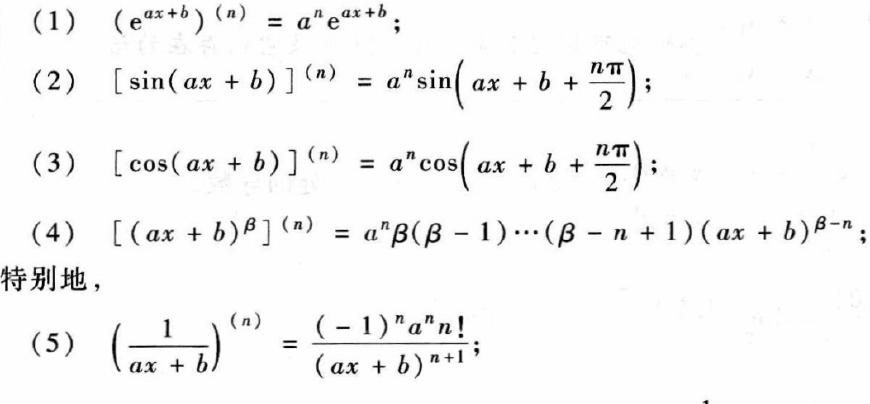
相关问题解答
-
指数函数求导公式怎么记比较容易呢?
说真的,记公式还是得多练多用,特别是(a^x)' = (ln a) a^x,想象一下你在“偷听”指数的秘密,它就躲在ln a里,超级酷炫!平常多写写,多默写,慢慢就烂熟于心啦! -
为什么e^x的导数还是e^x呢?
嘿,这可是e^x的独特魅力!它的变化率和函数值一模一样,简直就是数学界的“百搭王”,任何时候它都不带变臉,导数就是自己,简直帅呆了! -
学习高中导数公式有什么好方法?
哎呀,别紧张,关键是要多做题,多总结!还有,可以用“小卡片”背公式,找生活中的例子联想,或者和朋友一起讨论,学起来才不枯燥,记忆效率倍儿棒! -
复合函数求导法则怎么理解?
把复合函数想象成“套娃”,外面的套娃和里面的小娃娃都得拆开求导,然后把它们的导数乘起来,这就是链式法则啦。虽然听起来复杂,实际上一点儿也不难,多练习,信我,妥妥的轻轻松松!









新增评论