说到函数,咱们先来聊聊它的定义吧!简单来说,函数就是两个变量之间的一种“特殊关系”。
1. 传统定义告诉我们,假如你有两个变量x和y,当x在某个区间里取不同值时,y都能唯一地对应一个值,这时候我们就说y是x的函数,x叫做自变量。是不是很直观呢?
2. 近代的定义则从集合和映射的角度出发:给定两个非空集合A和B,一个规则f规定了集合A里任意元素x对应集合B里的唯一元素y,我们把这个映射f称作函数,记作y=f(x)。就是说,只要你给我一个x,我就能用这个规则找到唯一的y。
别忘啦,函数包含三个核心要素:
- 定义域A,就是输入的集合,决定了哪些x能进来凑热闹;
- 值域B,就是输出集合,包含所有可能的y;
- 还有最重要的——对应法则f,负责把x和y联系起来。
所以,函数本质上就是一条把每个输入和独一无二的输出“拉钩”约定好的规则,酷吧!
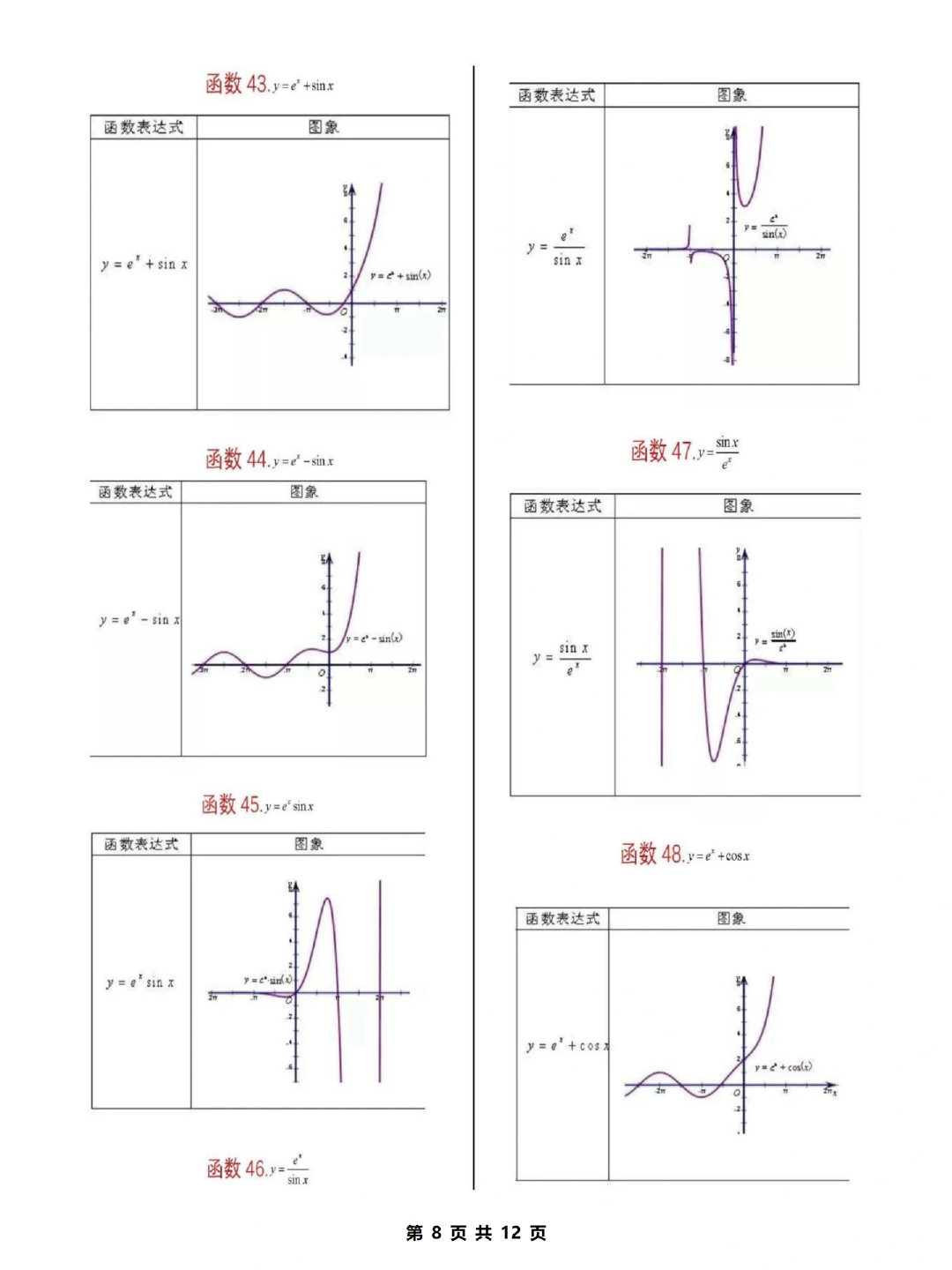
嘿,讲完它是啥,我们来看看函数咋表达,方便你我交流和算算。其实,函数的表示方式并不复杂,主要就是几种你经常遇到的格式:
1. y = f(x):这是最经典的形式,意思很清楚,“y凭借规则f跟x挂钩”。比如y=2x+3,这不就是函数嘛?
2. 映射写法f:A→B:这个有点书面化,强调的是从集合A到集合B的映射关系,听起来高大上一点,其实就是函数的“官方版”。
3. 表达式与图像:函数不仅可以用公式表示,还能画成图形,帮你一眼看出x和y的关系变化。
说白了,任何你能用来描述“每个x有且只有一个y对应它”的方法,都算得上是函数的表达。必须得提醒哈,不能有一个x配多个y,那就不算函数啦!
函数的定义为什么要唯一对应呢?
答:诶,你别小看这个唯一对应,它可是一条“铁律”!要是一个x对应好几个y,那就乱套了,根本没法确定到底哪个y是答案,函数可就不成立啦。唯一对应保证了每个输入都有确定的输出,让函数规则清晰明了,不糊弄人,这样用起来也不头疼。
函数值域和定义域有什么区别?
答:嘿,这俩东西其实就是函数输入和输出的家底!
定义域呢,简单说就是函数允许“进门”的所有x,没在定义域,函数就不认;
值域嘛,就是函数“欢迎”的所有y,也就是你能获得的各种输出值。理解它们,能帮你更准确地玩转函数。
函数和映射有什么不同吗?
答:说实话,这俩几乎是亲兄弟!“映射”是更广义的说法,泛指任何集合之间的对应规则,而“函数”通常是数学中特别强调对应唯一性的映射,尤其是数集之间的。别被这些术语难倒了,核心都是“对应关系”,我们日常用函数多点。
如何快速判断一个关系是不是函数呢?
答:这个嘛,最实用的招就是“垂直线测试”!想象一根铅笔竖着扫过你的图像,如果哪儿碰到不止一个点,那可就不是函数啦。这个小技巧超管用,简单直观,给你秒懂函数是不是成立哦!
添加评论