定积分求解技巧 分部积分法详细解析

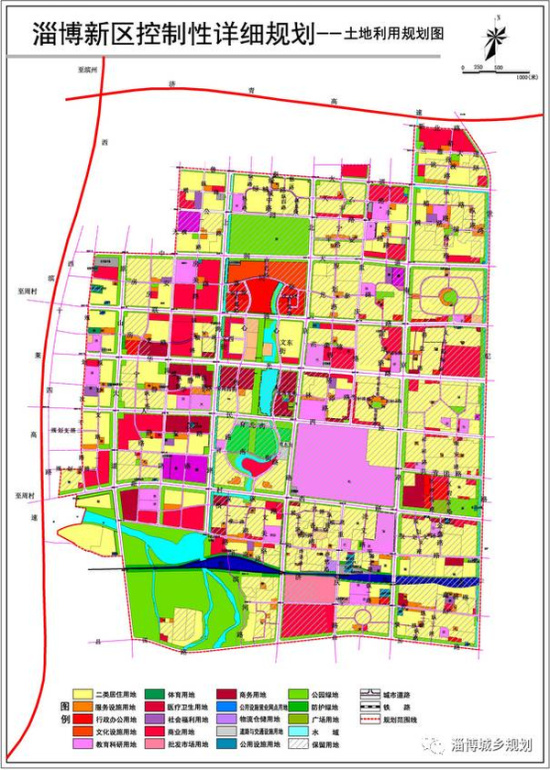
求大佬详细解这道定积分题目用分部积分法尽量详细点 计算过程步骤解析

该定积分题等于0.04404，咱们一步步拆解哈！首先得进行积分代换，令u=y²，这样被积函数就变成了ue^(-u)。接着上分部积分法这个大招，套公式∫udv=uv-∫vdu。具体操作时，先把xe²ˣdx写成1/2∫xde²ˣ，然后令u=x，v'=e²ˣ，这样u'=1，v=e²ˣ。哇塞，一下子就把积分变成xe²ˣ-∫e²ˣdx，超方便有木有！

积分求解方法与关键注意事项

1. 分部积分法的核心应用：比如解∫e^xsinxdx这种题，得先用凑微分法把e^x看成d(e^x)，再套分部积分公式。有时候算一次不够，还得重复操作，最后把含∫e^xsinxdx的项挪到左边合并，答案就出来啦！

2. 特殊函数的处理技巧：像e^(x^2)这种积分，哎呀，直接积分搞不定，得用极坐标变换或者高斯函数这些高级方法。平时做题时，记住不是所有函数都能用初等函数表示，灵活应变很重要哦。

3. 直接积分法的熟练关键：关键在于理解原函数定义和性质，会求简单函数的原函数。注意哈，先用分部积分，再用凑微分法变换，这样效率更高。别忘了不定积分的几何意义是求面积，超实用的！

4. 积分求面积的方法：基本积分法直接用公式计算，分部积分法则选好u和dv，按公式∫(u乘v)dx=u∫vdx-∫(u'∫vdx)dx操作。举个例子，求细杆转动惯量时，用积分法取质量元dl，套公式I=∫r²dm，超直观！

相关问题解答

1. 分部积分法最适合解决哪些类型的积分问题?

哈哈，分部积分法超适合处理乘积形式的函数积分，比如x乘以指数函数或者三角函数这种组合。当你看到∫xeˣdx或者∫xsinxdx这类题目，直接上分部积分准没错！记住口诀“反对幂三指”选择u的顺序，保你事半功倍～

2. 计算定积分时容易犯哪些错误?

哎呦，常见的坑可多了！比如忘了换限、代换后没回代、或者分部积分时符号搞反。还有啊，计算e^(x²)这种积分时，硬要用初等函数表达反而会错。大家记得多检查步骤，慢慢算别心急！

3. 如何用积分法求平面图形的面积?

超简单的！只要掌握定积分的几何意义——求曲线和坐标轴围成的面积。具体操作时，先确定积分上下限，再写出被积函数，直接算就行。比如求y=x²在[0,1]的面积，用∫₀¹x²dx，三两下就搞定啦！

4. 转动惯量积分计算有什么实用技巧?

嘿嘿，物理里的转动惯量其实用积分超好算！比如细杆绕端点的转动惯量，先设线密度ρ，取一小段dl，dm=ρdl，然后I=∫r²dm。实际计算时，代入上下限积分，结果就出来了。记得单位别搞错，不然物理老师要扣分哦～